I planted 16 F2 plants to test whether a marker is significant in this population. I get about 4 plants of AA and 4 plants of BB, and I did the T-test between AA and BB group, but I found the pvalue is only about 0.08. Should I reject the null hypothesis that AA and BB are the same? I probably will, but this experiment has too few samples, so I do not have enough statistical power to reject the null hypothesis.
After a search, I found we could estimate the sample size we need in order to get a significance level, say $\alpha = 0.001$. We just need to provide the desired significance level ($\alpha$), the sample mean difference between the two groups (based on our first experiment or some other priori), the standard deviation of the population, and the desired power ($1 - \beta$, the possibility it is real, $\beta$ is type II error). This website has some detailed information.
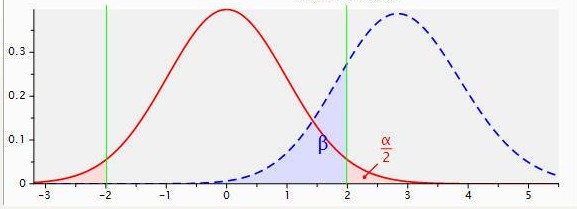Credit: https://stats.idre.ucla.edu/other/gpower/power-analysis-for-two-group-independent-sample-t-test/
There is also a good website for sample estimate. Here I just remade the wheel for my practice. The formula I used to calculate the sample size n is this (one tail):
$$n = (Z_\alpha + Z_\beta)^2 \frac{2\sigma^2}{d^2}$$
where $Z_\alpha$ and $Z_\beta$ are the critical value of the Normal distribution at $\alpha$ and $\beta$, respectively (e.g. for a confidence level of 95%, $\alpha$ is 0.05 and the critical value is 1.64; for a power of 80%, $\beta$ is 0.2 and the critical value is 0.84), $\sigma^2$ is the population variance, and d is the difference between the two groups.
Enter parameters below to estimate the required sample size
For example, in the experiment I mentioned, the group mean difference between AA and BB is about 2, standard deviation is about 1.2, and I want significant level $\alpha = 0.001$ (right tail, because I want AA - BB = 2), so the required sample size for each group is about 11, therefor I need to plant about 11 x 4 = 44 F2 plants.